How likely that someone we know dies from COVID-19?

The pandemic caused by the SARS-CoV-2 virus continues to spread and dominate daily life in 2020. Yet, despite the alarming numbers reported (“X millions of cases!”) it can feel abstract. As humans, we tend to care a lot more about our tribe than about anonymous people. With that in mind, what is the probability someone we care about dies from COVID-19?

First we need to define what caring about means: the average number of meaningful, stable social connections one can make (known as Dumbar’s number) is estimated around $150$. Even in our modern, hyperconnected world, it is hard to argue that it goes beyond $10^3$ individuals. In other words, individually we care about an extremely small fraction ($< 0.00001\%$) of humanity. A straightforward estimate of the probability $P$ of at least one of those contacts dying is given by:

\begin{equation} P = 1 - \left(1-R\times CFR\right)^K \end{equation}

where $K$ is the number of people we know, $R$ is the fraction of the population infected, and CFR is the Case Fatality Rate of the disease. Estimating both $R$ and CFR is currently extremely challenging: $R$ suffers from undersampling bias due to lack of testing, while $CFR$ in addition depends heavily on factors such as age, hospital infrastructure, and comorbidities. See [1] for a comprehensive discussion. Nevertheless, using $CFR=1.38\%$ [2], we find:

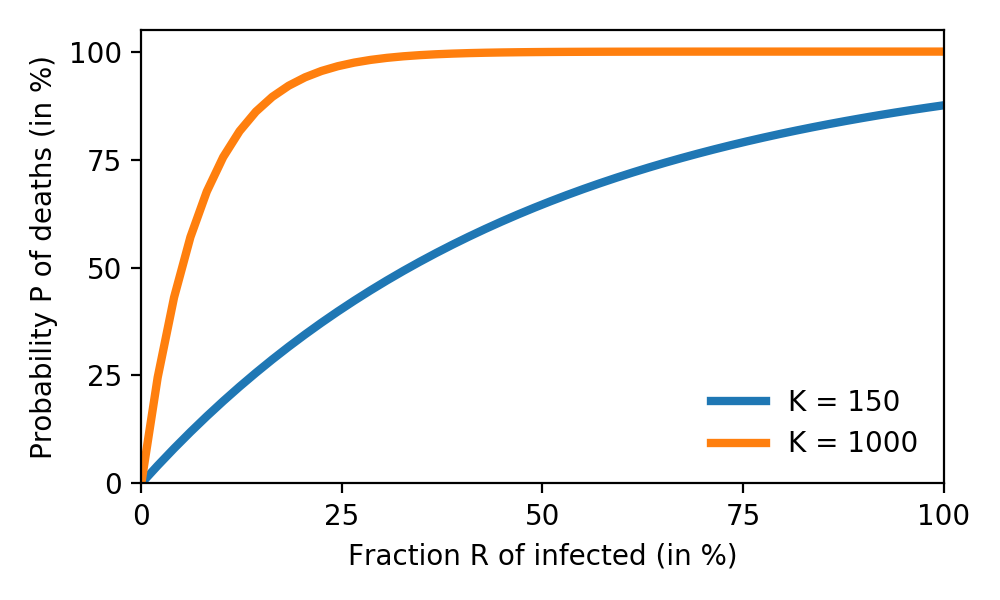Fig. 1: Probability $P$ of death of someone known from COVID-19, as function of the fraction of infected population $R$ and number of known people $K$.

We see that, as the disease spreads, eventually someone we know is likely to die from it. Knowing more people makes it happen sooner. With the estimated $CFR=1.38\%$, for $K=150$ the threshold where $P \geq 50\%$ (more likely to have a death than not) happens around $33\%$ infected. For $K=1000$ it is at $5\%$ infected. This can help explain some of the skepticism around COVID-19: as of writing, no country has reported infection rates close to those numbers (which would be catastrophic), and thus most people are simply not directly affected by a COVID-19 death.

There is a considerable dependence of Fig. 1 on the estimated $CFR$, however. If we calculate the necessary fraction of infection $R$ to make a death equally likely ($P=0.5$), we obtain:

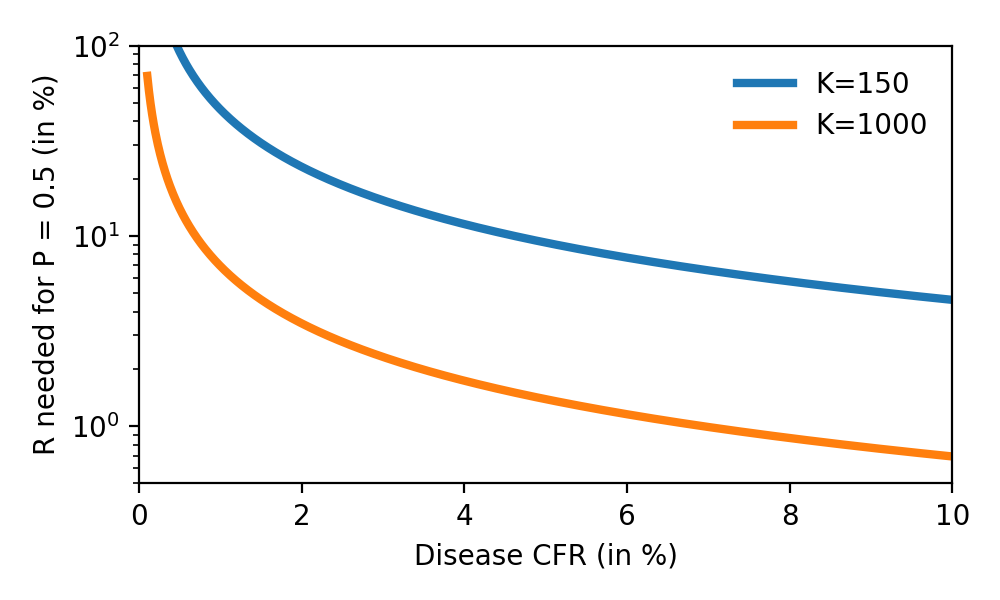Fig. 2: Dependency on the $CFR$ of the fraction of infection $R$ in order to make a death equally likely ($P=0.5$).

We find that, for larger estimates of the CFR still in a reasonable range, highly connected people ($K=1000$) are likely to start observing deaths with a fraction of infection under $1\%$. Most people ($K=150$), however, still would not observe deaths until infection reaches $\approx 10\%$.

We can improve the analysis a bit. As mentioned, the CFR depends heavily on age, with much higher fatality rates among the elderly. While there are large uncertainties and likely systematic biases in estimating the CFR, values obtained from different countries all follow the same trend [1].

A better estimate for the probability of death then takes into account both the age dependency of the CFR, and the age distribution (also known as population pyramid) of a given society. We assume that cases are spread homogeneously in the population, and that the age of the people we know follows the age distribution of the general population. With this, our expression for $P$ becomes:

\begin{equation} P = 1 - \left(1-R \sum_i f_i\times CFR_i \right)^K \end{equation}

where $CFR_i$ and $f_i$ are respectively the CFR and fraction of the population in age group $i$. We here use the CFR estimated from the initial outbreak in China:

Table 1: dependency of the $CFR$ on age during the outbreak in China. Taken from [3].

Lets consider the US, Brazil and Italy, all COVID-19 hotspots with considerably different population pyramids:

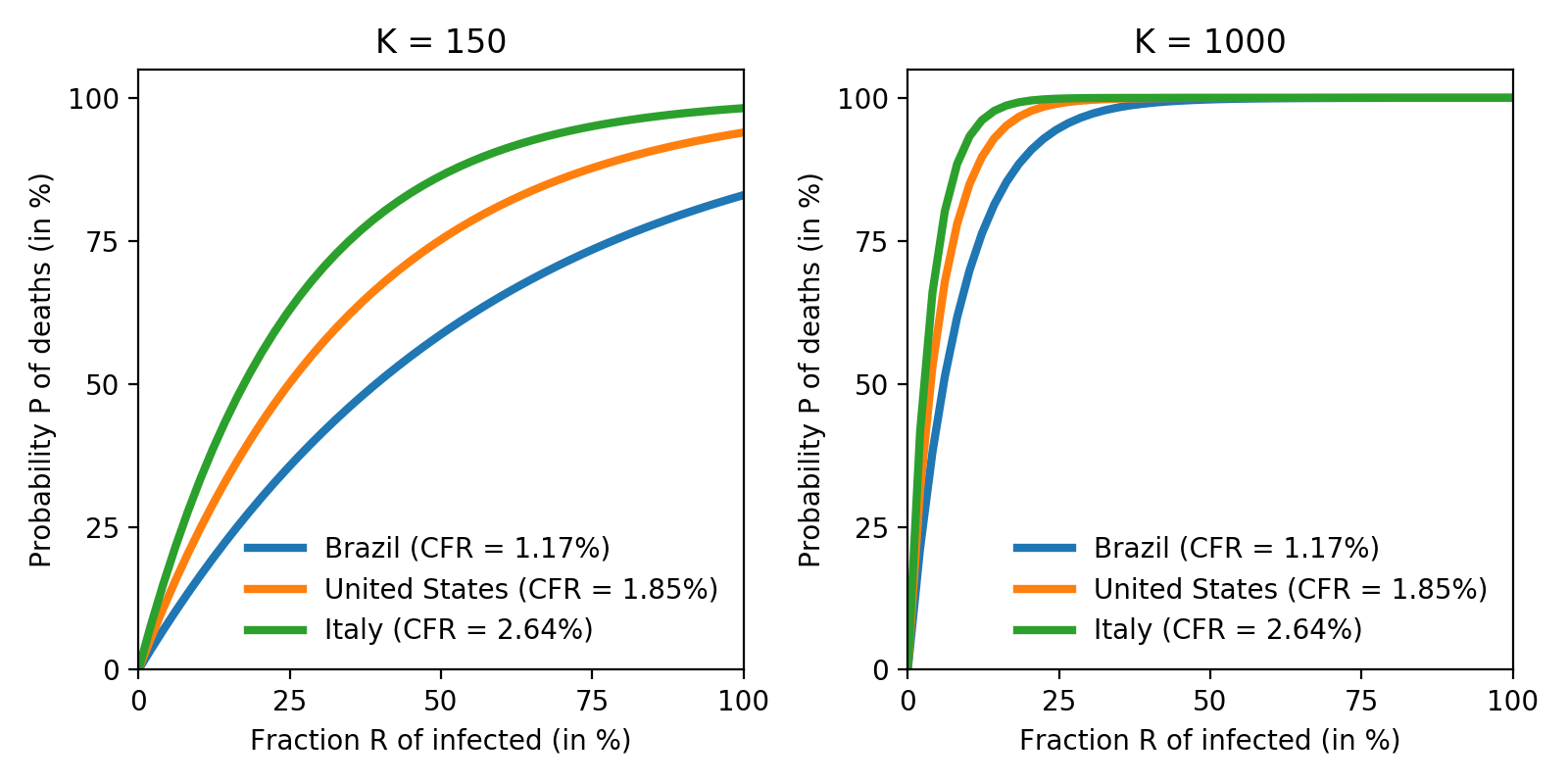Fig. 3: Probability $P$ of a death from COVID-19 for Brazil, the United States and Italy, with number of contacts $K=150$ (left) and $K=1000$ (right). Population pyramid data taken from [4].

We find that the pandemic hits home considerably earlier in Italy than it does in the US and Brazil. For the average person ($K=150$), the point were $P=0.5$ happens at around $17\%$ infected in Italy, but only around $40\%$ infected in Brazil.

In effect, COVID-19 mortality is dominated by the older population: while people aged 70+ are $17.1\%$ of the Italian population, they are only $10.9\%$ and $5.9\%$ of the population in the US and Brazil, respectively. This more than doubles the total CFR in Italy ($2.64\%$) compared to Brazil ($1.17\%$). The fact that the vast majority of deaths is among the older population is observed in other countries. See [5] for up-to-date figures on mortality in Germany, and [6] for data on CFR around the world.

In conclusion, this simple analysis shows somewhat of a tragic side of the COVID-19 phenomena: in order to take it seriously, many people need to be personally affected by the pandemic. Yet, due to the very small (relative) size of our social networks, this is unlikely to happen until it is far too late.

References:

1. https://ourworldindata.org/mortality-risk-covid
2. Verity et al. “Estimates of the severity of coronavirus disease 2019: a model-based analysis”. The Lancet Infectious Diseases 2020. DOI: 10.1016/S1473-3099(20)30243-7
3. Epidemiology Working Group for NCIP Epidemic Response, Chinese Center for Disease Control and Prevention. Zhonghua Liu Xing Bing Xue Za Zhi. 2020;41(2):145‐151. DOI:10.3760/cma.j.issn.0254-6450.2020.02.003
4. PopulationPyramid.net
5. https://joaopn.github.io/covid19/
6. https://www.cebm.net/covid-19/global-covid-19-case-fatality-rates/